FP2級過去問題 2017年9月学科試験 問3
問3
ライフプランニングにおける各種係数を用いた必要額の算出に関する次の記述の空欄(ア)、(イ)にあてはまる数値の組み合わせとして、最も適切なものはどれか。なお、算出に当たっては下記<資料>の係数を乗算で使用するものとし、手数料や税金等については考慮しないものとする。
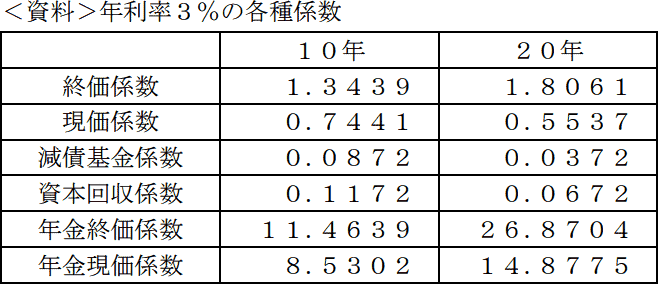
毎年年末に一定額を積み立てながら年利率3%で複利運用した場合、20年後に1,500万円となる貯蓄計画においては、毎年の積立金額は(ア)円となる。また、年利率3%で複利運用しながら、毎年年末に200万円を10年間受け取る場合においては、当初の元金として(イ)円が必要となる。

- (ア)558,000 (イ)17,060,400
- (ア)558,000 (イ)14,877,500
- (ア)744,100 (イ)17,060,400
- (ア)744,100 (イ)14,877,500
広告
広告
正解 1
問題難易度
肢177.8%
肢210.4%
肢39.8%
肢42.0%
肢210.4%
肢39.8%
肢42.0%
分野
科目:A.ライフプランニングと資金計画細目:3.ライフプランニングの考え方・手法
解説
資金計画を立てる際に用いる係数には以下の6つがあります。- 終価係数
- 現在の金額を一定利率で複利運用した場合のn年後の元利合計額を求める
- 現価係数
- 一定利率で複利運用するとして、n年後に一定金額に達するために必要な元本を求める
- 年金終価係数
- 毎年一定金額を積み立てた場合のn年後の元利合計額を求める
- 減債基金係数
- n年後に一定金額に達するために必要な毎年の積立額を求める
- 資本回収係数
- 現在の金額をn年間で取り崩した場合の毎年の受取額を求める
- 年金現価係数
- n年間にわたり一定金額を受け取るために必要な元本を求める
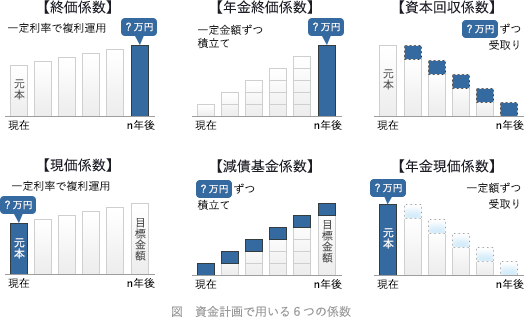
「毎年積み立てる」とくれば、使うのは「年金終価係数」または「減債基金係数」のどちらかです。設問のケースでは目標金額に達するために必要な「毎年の積立額」を知りたいので「減債基金係数」を用いるのが適切です。
表中の20年の場合の減債基金係数0.0372を用いて、
1,500万円×0.0372=558,000円
〔(イ)について〕
「毎年均等に取り崩して受け取る」とくれば、使うのは「資本回収係数」または「年金現価係数」のどちらかです。設問のケースでは毎年の取り崩す金額が決まっており、それを達するために必要な元本を知りたいため「年金現価係数」を用います。
表中の10年の場合の年金現価係数8.5302を用いて、
200万円×8.5302=17,060,400円
以上より[1]の組合せが適切です。
広告
広告