FP2級 2017年9月 実技（金財:個人）問3
問3
Aさんは、X社から支給される予定の退職金のうち、2,000万円を活用して老後資金を準備したいと考えている。そこで、Mさんは、諸係数早見表を用いてシミュレーションを行った。下記の係数を用いて、次の空欄①、②に入る最も適切な数値を解答用紙に記入しなさい。なお、答はそれぞれ万円未満を四捨五入して万円単位とし、税金や手数料等は考慮しないものとする。また、問題の性質上、明らかにできない部分は「□□□」で示してある。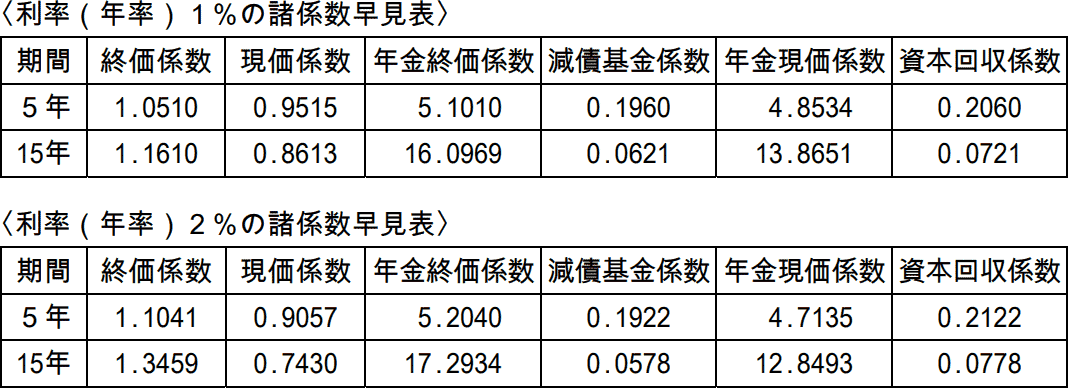
- 元金2,000万円を、利率（年率）2％で5年間複利運用する場合、5年後の元利合計金額はいくらか。
2,000万円×□□□＝□□□円 ⇒（①）万円 - 上記1で求めた金額（万円未満を四捨五入した後の金額）を、利率（年率）1％で複利運用しながら、15年間にわたって毎年一定額を取り崩す場合、毎年の取崩し金額（上限）はいくらか。
（①）万円×□□□＝□□□円 ⇒（②）万円
| ①万円 |
| ②万円 |
広告
正解
| ① 2,208（万円） |
| ② 159（万円） |
分野
科目：A.ライフプランニングと資金計画細目：3.ライフプランニングの考え方・手法
解説
〔①について〕
一定の元本を複利運用した将来の金額を計算する場合は「終価係数」を使います。
＜利率（年率）＞2％の諸係数早見表から、期間5年の終価係数をみると1.1041になっているので、
2,000万円×1.1041＝2,208.2万円
（万円未満を四捨五入して）2,208万円
よって、正解は2,208(万円)になります。
〔②について〕
元本を一定利率で複利運用しながら毎年一定額を取り崩す場合に、毎年いくら受け取れるかを計算するときは資本回収係数を使います。
①の答えの2,208万円に、年率1％・期間15年の資本回収係数を乗じます。
2,208万円×0.0721＝159.1968万円
（万円未満を四捨五入して）159万円
よって、正解は159(万円)になります。
一定の元本を複利運用した将来の金額を計算する場合は「終価係数」を使います。
2,000万円×1.1041＝2,208.2万円
（万円未満を四捨五入して）2,208万円
よって、正解は2,208(万円)になります。
〔②について〕
元本を一定利率で複利運用しながら毎年一定額を取り崩す場合に、毎年いくら受け取れるかを計算するときは資本回収係数を使います。
2,208万円×0.0721＝159.1968万円
（万円未満を四捨五入して）159万円
よって、正解は159(万円)になります。
広告