FP2級 2019年5月 実技(FP協会:資産設計)問28
問28
政彦さんは、現在居住している自宅の住宅ローン(全期間固定金利、返済期間35年、元利均等返済、ボーナス返済なし)の繰上げ返済を検討しており、FPの榎田さんに繰上げ返済について質問をした。政彦さんが住宅ローンを132回返済後に、100万円以内で期間短縮型の繰上げ返済をする場合、この繰上げ返済により短縮される返済期間として、正しいものはどれか。なお、計算に当たっては、下記<資料>を使用し、繰上げ返済額は100万円を超えない範囲での最大額とすること。また、繰上げ返済に伴う手数料等は考慮しないものとする。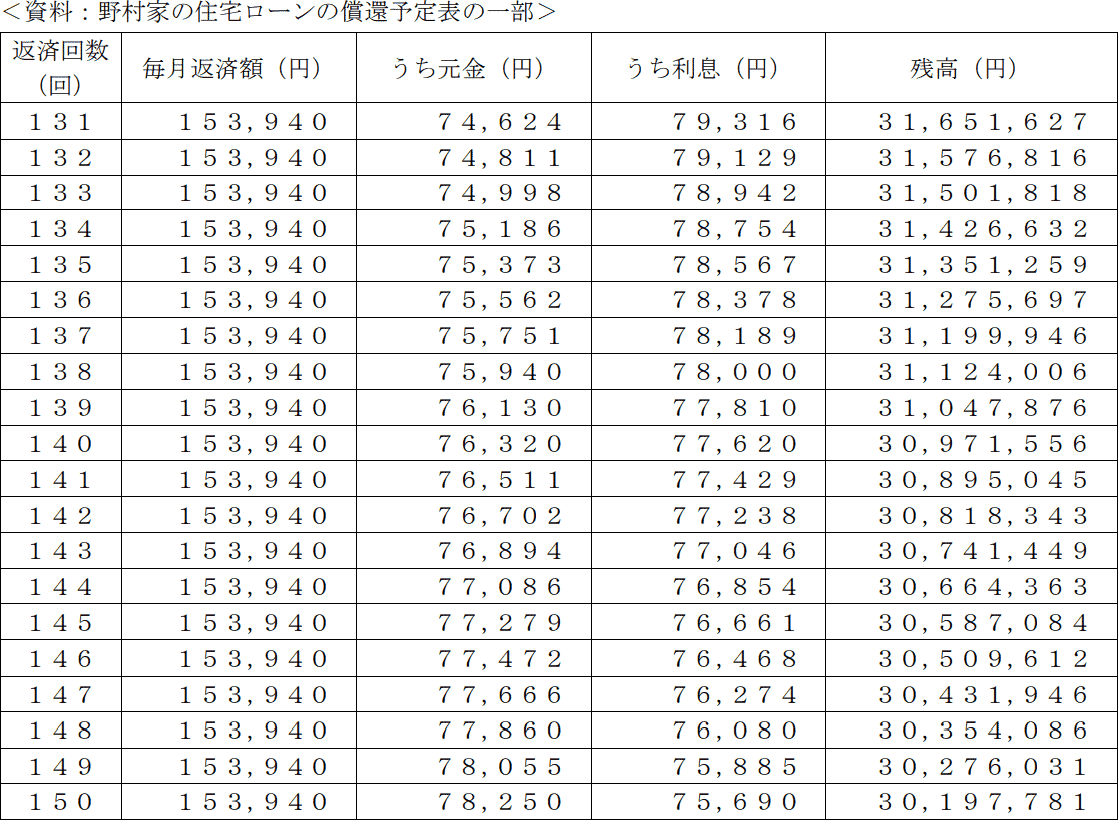

- 6ヵ月
- 1年0ヵ月
- 1年1ヵ月
- 1年2ヵ月
広告
広告
正解 3
分野
科目:A.ライフプランニングと資金計画細目:8.ライフプラン策定上の資金計画
解説
<資料>より132回返済後の残高は31,576,816円です。
ここで100万円を繰上げ返済をすると、借入残高は「31,576,816円-1,000,000円=30,576,816円」まで減ります。繰上げ返済額は次回返済分から順に元金部分に充当されるので、<資料>のうち残高が30,576,816円以上となっている返済回までは、返済を完了できることになります。
<資料>を見ると、残高が30,576,816円以上であり、最も先の返済回は145回目(30,587,084円)と確認できます。このことから、100万円の繰上げ返済をすると133回目から145回目までの13回分について元金を全額返済できるとわかります。全額返済された月の分だけ返済期間が短縮されるので、短縮される返済期間は「13ヶ月=1年1ヶ月」となります。
したがって正解は[3]です。
また、次のような方法でも解答を導くことができます。
ここで100万円を繰上げ返済をすると、借入残高は「31,576,816円-1,000,000円=30,576,816円」まで減ります。繰上げ返済額は次回返済分から順に元金部分に充当されるので、<資料>のうち残高が30,576,816円以上となっている返済回までは、返済を完了できることになります。
<資料>を見ると、残高が30,576,816円以上であり、最も先の返済回は145回目(30,587,084円)と確認できます。このことから、100万円の繰上げ返済をすると133回目から145回目までの13回分について元金を全額返済できるとわかります。全額返済された月の分だけ返済期間が短縮されるので、短縮される返済期間は「13ヶ月=1年1ヶ月」となります。
したがって正解は[3]です。
また、次のような方法でも解答を導くことができます。
- 133回目から順に元金返済額を足し算していき、繰上げ返済額に達するまでの月数を数える
- 繰上げ返済額を、元金返済額のおおよその平均値で割る
広告
広告