FP2級過去問題 2024年1月学科試験 問27

問27

ポートフォリオ理論に関する次の記述のうち、最も不適切なものはどれか。
  1. システマティック・リスクは、市場全体の変動の影響を受けるリスクであり、分散投資によっても消去しきれないリスクとされている。
  2. ポートフォリオのリスクは、組み入れた各資産のリスクを組入比率で加重平均した値以下となる。
  3. 異なる2資産からなるポートフォリオにおいて、2資産間の相関係数が－1である場合、ポートフォリオを組成することによる分散投資の効果（リスクの低減）は得られない。
  4. 同一期間における収益率が同じ2つのファンドをシャープ・レシオで比較する場合、収益率の標準偏差の値が小さいファンドの方が、収益率の標準偏差の値が大きいファンドよりも当該期間において効率的に運用されていたと評価することができる。
1234
広告

正解　3

問題難易度
肢17.1%
肢28.1%
肢374.3%
肢410.5%

分野

科目：C.金融資産運用
細目：9.ポートフォリオ運用

解説

  1. 適切。システマティック・リスクとは市場全体の動きの影響を受けるリスクで、分散投資によっても軽減することはできません。これに対して、分散投資をすることによって低減できるリスクを、アン・システマティック・リスクといいます。
    システマティック・リスクは、市場全体のリスクの影響を受けるリスクであり、分散投資によっても軽減することができないとされている。（2015.9-27-2）
  2. 適切。ポートフォリオの期待収益率は、組み入れた各資産の期待収益率を組入比率で加重平均した値となります。加重平均とは、値ごとに割合を重み付けして平均する方法です。
    たとえば、A資産（期待収益率2.5％）を40％、B資産（期待収益率6.0％）を60％の割合で保有しているとします。40％・60％が組入比率です。このとき、ポートフォリオの期待収益率は以下のように計算します。
    • A資産　2.5％×0.4＝1％
    • B資産　6.0％×0.6＝3.6％
    • 加重平均した値　1％＋3.6％＝4.6％
    ポートフォリオのリスクは、組み入れた各資産のリスクを組入比率で加重平均した値以下となる。（2023.9-28-1）
    ポートフォリオのリスクは、組み入れた各資産のリスクを組入比率で加重平均した値以下となる。（2022.5-28-4）
    ポートフォリオのリスクは、組み入れた各資産のリスクを組入比率で加重平均した値よりも大きくなる。（2021.1-27-4）
    ポートフォリオのリスクは、組み入れた各資産のリスクを組入比率で加重平均した値よりも大きくなる。（2020.1-27-3）
  3. [不適切]。2つの資産間の値動きの関連性を数値化したものを相関係数といい、「1」から「－1」までの数値で表します。相関係数が「－1」の資産同士は全く逆の値動きをするので最大のリスク低減効果を得られます。
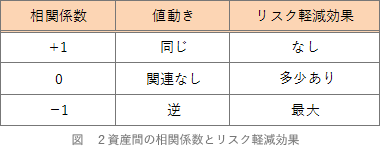    3/900.png/image-size:380×146
    異なる2資産からなるポートフォリオにおいて、2資産間の相関係数がゼロである場合、ポートフォリオを組成することによる分散投資の効果（リスクの低減効果）は生じない。（2022.5-28-2）
    異なる2資産からなるポートフォリオにおいて、2資産間の相関係数が－1の場合、ポートフォリオを組成することによる分散投資の効果（リスクの軽減）は得られない。（2021.3-29-2）
    異なる2資産からなるポートフォリオにおいて、2資産間の相関係数が－1である場合、ポートフォリオを組成することによる分散投資の効果（リスクの低減）は得られない。（2021.1-27-2）
    異なる2資産からなるポートフォリオにおいて、2資産間の相関係数が1である場合、ポートフォリオを組成することによる分散投資の効果（リスクの低減効果）は最大となる。（2020.1-27-2）
    異なる2資産からなるポートフォリオにおいて、2資産間の相関係数が－1となる場合、ポートフォリオを組成することによる分散投資の効果（リスクの低減）は得られない。（2018.5-28-4）
    異なる2資産からなるポートフォリオにおいて、2資産間の相関係数が1となる場合、ポートフォリオを組成することによる分散投資の効果（リスクの低減）は最大となる。（2017.1-27-1）
    異なる2資産からなるポートフォリオにおいて、2資産間の相関係数が－1となる場合、ポートフォリオを組成することによる分散投資の効果（リスクの軽減）は得られない。（2016.9-27-2）
    異なる2資産からなるポートフォリオにおいて、2資産間の相関係数が-1の場合、ポートフォリオを組成することによる分散投資の効果（リスクの軽減）は得られない。（2016.5-29-2）
    異なる2資産からなるポートフォリオにおいて、2資産間の相関係数が1となる場合、ポートフォリオを組成することによる分散投資の効果（リスクの軽減）は最大となる。（2015.10-28-1）
    異なる2資産からなるポートフォリオにおいて、2資産間の相関係数が0（ゼロ）の場合、ポートフォリオを組成することによる分散投資効果は得られない。（2015.9-27-3）
    異なる2資産からなるポートフォリオにおいて、2資産間の相関係数が0（ゼロ）の場合、ポートフォリオ効果は得られず、ポートフォリオのリスクは単純に投資割合で加重平均したものになる。（2014.1-29-2）
  4. 適切。シャープレシオは、リスク（標準偏差で表す）に比してどれだけ効率的にリターン（収益）を得ることができたかを見る指標で、以下の式で求めます。
    　収益率－無リスク資産の収益率標準偏差
    収益率が同じであれば、分母である標準偏差の値が小さいほど、シャープレシオの数値は大きくなります。シャープレシオが大きいほど効率よく運用されたと評価されます。
    同一期間の収益率がプラスで、かつその数値が同じである2つのファンドをシャープレシオで比較した場合、収益率の標準偏差の値が小さいファンドの方が効率よく運用されていたと評価することができる。（2021.3-29-3）
    同一期間の収益率が同じ2つのファンドをシャープレシオで比較した場合、収益率の標準偏差の値が小さいファンドの方が、取ったリスクに対して効率的に運用されていたと評価することができる。（2015.10-28-4）
    同一期間の収益率が同じ2つのファンドをシャープレシオで比較した場合、収益率の標準偏差の値が小さいファンドの方が効率よく運用されていたと評価することができる。（2015.9-27-4）
    同一期間の収益率が同じ2つのファンドをシャープレシオで比較した場合、収益率の標準偏差の値が小さいファンドの方が効率よく運用されていたと評価することができる。（2015.1-27-4）
    標準偏差は異なるが収益率が同じ2つのファンドをシャープレシオで比較した場合、標準偏差の値が大きいファンドの方が効率よく運用されていたと評価することができる。（2014.1-29-4）
したがって不適切な記述は[3]です。
広告