ポートフォリオ運用（全40問中14問目）

No.14

ポートフォリオ理論に関する次の記述のうち、最も適切なものはどれか。
2021年1月試験　問27
  1. 国内株式のポートフォリオにおいて、組入れ銘柄数を増やすことにより、システマティック・リスクを低減することができる。
  2. 異なる2資産からなるポートフォリオにおいて、2資産間の相関係数が－1である場合、ポートフォリオを組成することによる分散投資の効果（リスクの低減）は得られない。
  3. ポートフォリオの期待収益率は、組み入れた各資産の期待収益率を組入比率で加重平均した値となる。
  4. ポートフォリオのリスクは、組み入れた各資産のリスクを組入比率で加重平均した値よりも大きくなる。
1234
広告

正解　3

問題難易度
肢117.1%
肢29.3%
肢360.2%
肢413.4%

分野

科目：C.金融資産運用
細目：9.ポートフォリオ運用

解説

  1. 不適切。システマティック・リスク（市場リスク）とは、市場全体の動向から影響を受けるリスクのことで、組入れ銘柄数を増やして分散投資をしても軽減することはできません。
    国内株式のポートフォリオにおいて、システマティック・リスクは、ポートフォリオの組入れ銘柄数を増やしても低減しない。（2021.3-29-4）
    株式のポートフォリオにおいて、組入れ銘柄数を増やすことにより、システマティック・リスクを低減することができる。（2018.5-28-3）
    システマティック・リスクは、ポートフォリオの組入れ銘柄数を増やしても低減しない（2017.1-27-4）
    株式のポートフォリオへの組入れ銘柄数を増やすことにより、市場全体の動き（システマティック・リスク）の影響を軽減することができる。（2016.9-27-4）
    システマティック・リスクは、ポートフォリオの組入れ銘柄数を増やしても低減しない。（2016.5-29-4）
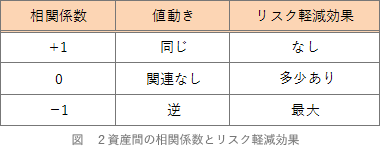
  2. 不適切。2資産間の相関係数が－1の場合、全く逆の値動きをするということなのでリスク低減効果は最大となります。
    3/900.png/image-size:380×146
    異なる2資産からなるポートフォリオにおいて、2資産間の相関係数が－1である場合、ポートフォリオを組成することによる分散投資の効果（リスクの低減）は得られない。（2024.1-27-3）
    異なる2資産からなるポートフォリオにおいて、2資産間の相関係数がゼロである場合、ポートフォリオを組成することによる分散投資の効果（リスクの低減効果）は生じない。（2022.5-28-2）
    異なる2資産からなるポートフォリオにおいて、2資産間の相関係数が－1の場合、ポートフォリオを組成することによる分散投資の効果（リスクの軽減）は得られない。（2021.3-29-2）
    異なる2資産からなるポートフォリオにおいて、2資産間の相関係数が1である場合、ポートフォリオを組成することによる分散投資の効果（リスクの低減効果）は最大となる。（2020.1-27-2）
    異なる2資産からなるポートフォリオにおいて、2資産間の相関係数が－1となる場合、ポートフォリオを組成することによる分散投資の効果（リスクの低減）は得られない。（2018.5-28-4）
    異なる2資産からなるポートフォリオにおいて、2資産間の相関係数が1となる場合、ポートフォリオを組成することによる分散投資の効果（リスクの低減）は最大となる。（2017.1-27-1）
    異なる2資産からなるポートフォリオにおいて、2資産間の相関係数が－1となる場合、ポートフォリオを組成することによる分散投資の効果（リスクの軽減）は得られない。（2016.9-27-2）
    異なる2資産からなるポートフォリオにおいて、2資産間の相関係数が-1の場合、ポートフォリオを組成することによる分散投資の効果（リスクの軽減）は得られない。（2016.5-29-2）
    異なる2資産からなるポートフォリオにおいて、2資産間の相関係数が1となる場合、ポートフォリオを組成することによる分散投資の効果（リスクの軽減）は最大となる。（2015.10-28-1）
    異なる2資産からなるポートフォリオにおいて、2資産間の相関係数が0（ゼロ）の場合、ポートフォリオを組成することによる分散投資効果は得られない。（2015.9-27-3）
    異なる2資産からなるポートフォリオにおいて、2資産間の相関係数が0（ゼロ）の場合、ポートフォリオ効果は得られず、ポートフォリオのリスクは単純に投資割合で加重平均したものになる。（2014.1-29-2）
  3. [適切]。ポートフォリオの期待収益率は、組み入れた各資産の期待収益率を組入比率で加重平均した値となります。加重平均とは、値ごとに割合を加味して平均する方法です。
    たとえば、A資産（期待収益率2.5％）を40％、B資産（期待収益率6.0％）を60％の割合で保有しているとします。40％・60％が組入比率です。このとき、ポートフォリオの期待収益率は以下のように計算します。
    • A資産　2.5％×0.4＝1％
    • B資産　6.0％×0.6＝3.6％
    • 加重平均した値　1％＋3.6％＝4.6％
    ポートフォリオの期待収益率は、組み入れた各資産の期待収益率を組入比率で加重平均した値よりも大きくなる。（2023.9-28-3）
    ポートフォリオの期待収益率は、組み入れた各資産の期待収益率を組入比率で加重平均した値となる。（2022.5-28-3）
    ポートフォリオの期待収益率は、組み入れた各資産の期待収益率を単純平均した値となる。（2022.1-27-4）
    ポートフォリオの期待収益率は、ポートフォリオに組み入れた各資産の期待収益率を組入比率で加重平均した値となる。（2021.3-29-1）
    ポートフォリオの期待収益率は、組み入れた各資産の期待収益率を組入比率で加重平均した値よりも大きくなる。（2020.1-27-4）
    ポートフォリオの期待収益率は、ポートフォリオに組み入れた各資産の期待収益率を組入比率で加重平均した値となる。（2018.5-28-1）
    ポートフォリオの期待収益率は、ポートフォリオに組み入れた各資産の期待収益率を組入比率で加重平均した値となる。（2016.5-29-1）
    ポートフォリオの期待収益率は、ポートフォリオに組み入れた各資産の期待収益率を組入比率で加重平均して得た値となる。（2015.9-27-1）
    ポートフォリオの期待収益率は、ポートフォリオに組み入れた各資産の期待収益率を組入比率で加重平均して得た値となる。（2015.1-27-1）
  4. 不適切。ポートフォリオのリスクは、相関係数が1でない限り、組み入れた各資産のリスクを組入比率で加重平均した値よりも小さくなります。これを「ポートフォリオ効果」といいます。
    ポートフォリオのリスクは、組み入れた各資産のリスクを組入比率で加重平均した値以下となる。（2024.1-27-2）
    ポートフォリオのリスクは、組み入れた各資産のリスクを組入比率で加重平均した値以下となる。（2023.9-28-1）
    ポートフォリオのリスクは、組み入れた各資産のリスクを組入比率で加重平均した値以下となる。（2022.5-28-4）
    ポートフォリオのリスクは、組み入れた各資産のリスクを組入比率で加重平均した値よりも大きくなる。（2020.1-27-3）
したがって適切な記述は[3]です。
広告